olrlobt
[알고리즘] Divide and Conquer Algorithm : 분할정복 알고리즘을 알아보자 본문
분할 정복 알고리즘 (Divide and Conquer Algorithm)
분할정복 알고리즘은 간단히 말해, 문제를 작게 분할한 후 각각을 정복하는 알고리즘이다.
큰 문제를 작은 문제로 분할하여 각각을 해결하고, 그 결과를 이용해 전체 문제를 해결한다.
이때 분할된 작은 문제는 원래 문제와 같은 형태를 가지며, 작은 문제는 원래 문제의 일부분이 된다. 분할된 작은 문제를 재귀적으로 해결하고, 이를 결합하여 원래 문제를 해결한다.
분할정복 알고리즘은 재귀적인 방법을 통해 문제를 해결하며, 대표적인 예시로는 이진 탐색(Binary Search), 병합 정렬(Merge Sort), 퀵 정렬(Quick Sort) 등이 있다.
분할 정복 알고리즘과 동적계획법(DP)
분할정복 알고리즘과 동적 계획법은 모두 대규모 문제를 해결하기 위한 알고리즘으로,
한 문제를 작게 나눈다는 점에서 유사한 접근 방법을 가지고 있다. 하지만, 목적과 사용 방법에 분명한 차이가 있다.
DP를 모른다면 아래 글을 참고하자.
https://olrlobt.tistory.com/29
[알고리즘] 동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming)
동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming) DP는 하나의 큰 문제를 작은 문제로 나눈 뒤, 기억하여 푸는 알고리즘 기법이다. DP에서 동적계획법, 동적프로그래밍이라는 단어는, DP 창시
olrlobt.tistory.com
분할정복 알고리즘은 문제를 작게 나누어 해결하고, 이 해결을 결합하여 원래의 문제를 해결한다. 또한 재귀를 이용하여 구현하는 것이 일반적이다. 따라서, 부분 문제들이 서로 독립적일 때 사용하기 좋다. 예를 들어, 정렬 알고리즘인 합병 정렬(Merge Sort)은 분할정복 알고리즘을 이용하여 구현된다.
반면, 동적 계획법은 하위 문제들을 한 번씩만 계산하고, 이를 이용하여 상위 문제를 효율적으로 계산하는 것에 목적을 둔다. 또한 반복문을 이용하여 구현하는 것이 일반적이다. 따라서, 부분 문제들이 서로 종속적일 때 사용하기 좋다. 예를 들어, 최단 경로 문제는 동적 계획법을 이용하여 해결할 수 있다.
문제의 특성에 따라 분할정복 알고리즘과 동적 계획법 중 적합한 알고리즘을 선택하여 사용하는 것이 중요하다.
분할정복 알고리즘 탐색과정
이 프로세스는 작게 분할한 문제가 직접 해결 가능할 만큼 충분히 작아질 때까지 재귀적으로 계속된다.
일반적으로 분할정복 알고리즘은 다음 세 단계로 구성된다.
- 분할: 문제를 작은 하위 문제로 분할.
- 정복: 각 하위 문제는 재귀적으로 해결.
- 결합: 하위 문제의 해결책을 결합하여 원래 문제를 해결.
분할정복 알고리즘을 사진으로 이해해 보기

위의 그림은 백준 1074번 문제 : Z이다.
문제는 간단하게, Z 모양으로 반복되는 패턴에서,
0행 0열부터 시작한다면, 3행 3열은 몇 번째 숫자를 나타 내는지를 구하는 문제이다.
이 문제를 분할정복을 이용하여 해결하여 보자.
먼저, 분할 단계이다. 숫자는 신경 쓰지 말고 사각형의 크기에만 집중해 보자.
위의 그림은 반복되는 패턴이 있으므로 4 등분하여 문제를 작게 분할하여 해결할 수 있다.
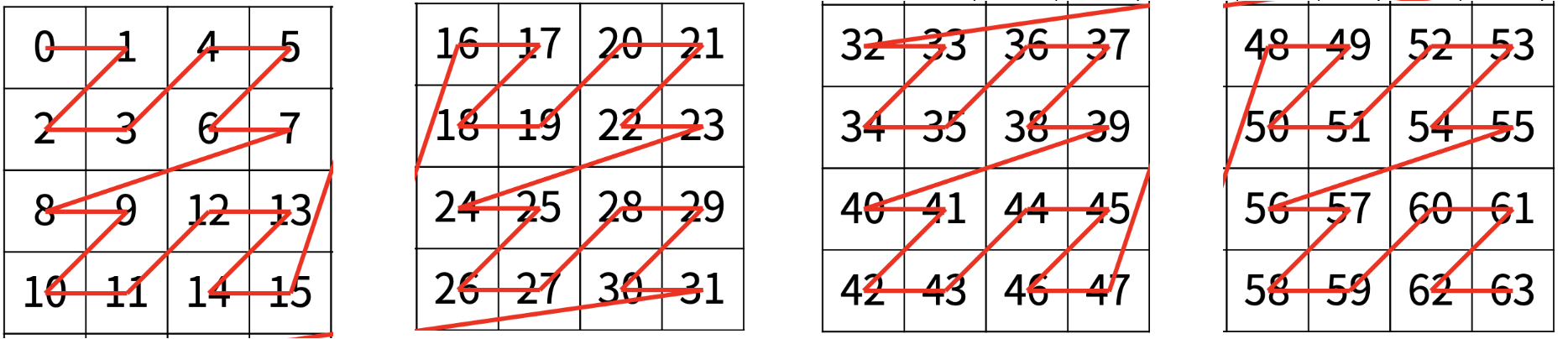
이 중, 구하고자 하는 3행 3열은 첫 번째 사각형에 위치한다. 하지만 3행 3열에 집중하지 말고, 사각형에만 집중해 보자.
그리고 이 사각형이 제일 작은 문제가 아니기 때문에, 똑같이 반복되는 패턴 4개로 작게 분할한다.

이 그림에서도 숫자가 아니라 사각형에 집중하자. 아직 가장 작은 문제가 아니므로 작게 분할할 수 있다.

이 것이 가장 작게 나눈 가장 작은 문제가 된다. 현재 그림에는 숫자가 쓰여 있어서 헷갈릴 수 있지만,
가장 작은 사각형 중에 네 번째 사각형이므로 실제 우리가 구한 값은 아래의 그림.

즉 해결 단계에서, 3의 값을 구한 것이다.
가장 작은 문제를 해결했으므로, 이제는 작은 문제들을 결합시킨다.

내가 구한 것은 가장 작은 문제에서 3의 값을 나타내지만, 이 작은 문제들의 결합인 위의 문제에서는
네 번째 그림을 나타낸다.
각 사각형의 첫 번째 값이 4 단위로 증가하기 때문에,
(가장 작은 사각형에서 구한 값 3) + (네 번째 사각형 4-1) x ( 단위 4) = 15의 값을 구할 수 있다.

마지막 위의 결합 부분에서는 구하고자 하는 결과가 첫 번째 사각형 이기 때문에, 그대로 15라는 답이 도출된다.
만약, 위 문제가 3행 3열이 아닌, 7행 3열을 구하는 문제였다면, 위 그림에서 세 번째 사각형에 위치한다.
각 사각형이 16 단위로 증가하기 때문에,
(이 전 사각형에서의 값 15) + ( 세 번째 사각형 3-1 ) x ( 단위 16) = 47의 값이 도출된다.
분할정복 알고리즘 장단점
분할정복 알고리즘 장점:
- 빠른 속도: 큰 문제를 작은 하위 문제로 분할하고 해결하여 전체 문제를 해결하는 데 걸리는 시간을 줄일 수 있다.
- 쉬운 병렬화: 분할정복 알고리즘은 하위 문제를 병렬로 처리하기 쉬우므로 멀티코어 시스템에서 성능을 크게 향상할 수 있다.
- 유연성: 이 알고리즘은 여러 응용 분야에서 사용될 수 있으며, 문제의 복잡도와 데이터 크기에 상관없이 적용할 수 있다.
분할정복 알고리즘 단점:
- 추가적인 메모리 요구: 알고리즘은 재귀적으로 호출되므로 많은 추가적인 메모리를 필요로 할 수 있다.
- 최악의 경우 시간 복잡도: 일부 문제에 대해서는 분할정복 알고리즘이 최악의 경우에도 빠른 해결책을 제공하지 못할 수 있다.
- 구현의 복잡성: 이 알고리즘은 구현이 비교적 복잡할 수 있으며, 종종 추가적인 문제를 발생시킬 수 있다.
분할정복 알고리즘은 많은 문제에 대해 매우 효과적이며, 많은 응용 분야에서 사용된다. 하지만 구현이 복잡하고 추가적인 메모리 요구가 있을 수 있으므로, 적용 전에 장단점을 고려해야 한다.
분할정복 알고리즘 구현
public class MaxValue {
public static int findMax(int[] arr, int low, int high) {
if (low == high) { // 배열의 길이가 1인 경우
return arr[low];
} else {
int mid = (low + high) / 2;
int leftMax = findMax(arr, low, mid); // 왼쪽 부분 배열에서 최댓값 찾기
int rightMax = findMax(arr, mid + 1, high); // 오른쪽 부분 배열에서 최댓값 찾기
return Math.max(leftMax, rightMax); // 두 부분 배열에서의 최댓값 반환
}
}
public static void main(String[] args) {
int[] arr = {5, 10, 7, 25, 15};
int max = findMax(arr, 0, arr.length - 1);
System.out.println("최댓값: " + max);
}
}
이 예시에서는 배열의 최댓값을 찾기 위해 findMax 메서드가 재귀적으로 호출한다.
먼저 배열의 길이가 1인 경우에는 해당 값을 반환하고, 그렇지 않은 경우에는 배열을 중간 지점을 기준으로 두 부분으로 분할하고 각 부분에서 최댓값을 찾는다.
마지막으로 두 부분에서의 최댓값을 비교하여 더 큰 값을 반환한다.
분할정복 알고리즘 시간복잡도
분할정복 알고리즘의 시간복잡도는 분할, 해결, 결합 세 가지 단계에서 각각의 연산량에 따라 결정된다. 이때 분할 단계에서는 분할의 수가 결정되므로, 분할된 작은 문제들의 크기와 관계없이 일정한 연산량을 가지게 된다. 일반적으로 분할된 작은 문제들의 수는 로그 함수의 형태를 가지며, 결합 단계에서의 연산량은 선형 함수의 형태를 가진다.
시간복잡도 : O(NlogN)
이 시간복잡도는 일반적인 분할정복 알고리즘의 시간복잡도로, 문제의 특성에 따라 달라질 수 있다.
예로, 앞서 말한 예시인 병합 정렬의 경우 O(NlogN)의 시간복잡도를 갖지만, 이진탐색의 경우 O(logN)의 시간 복잡도를 갖는다.
따라서 분할정복 알고리즘을 사용할 때에는 시간복잡도를 적절히 분석하여 알고리즘의 효율성을 검토해야 한다.
분할정복 알고리즘 예시문제
분할정복 알고리즘은 나에게 있어서 난도가 높게 느껴졌다. 따라서 백준 문제도 난이도를 기존보다 낮추어 풀었고, 아래 문제들은 내가 추천하는 분할정복 알고리즘 문제이다.
https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
https://www.acmicpc.net/problem/1992
1992번: 쿼드트리
첫째 줄에는 영상의 크기를 나타내는 숫자 N 이 주어진다. N 은 언제나 2의 제곱수로 주어지며, 1 ≤ N ≤ 64의 범위를 가진다. 두 번째 줄부터는 길이 N의 문자열이 N개 들어온다. 각 문자열은 0 또
www.acmicpc.net
https://www.acmicpc.net/problem/2447
2447번: 별 찍기 - 10
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다. 크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이
www.acmicpc.net
'Algorithm > 알고리즘 종류' 카테고리의 다른 글
| [알고리즘] Euclidean Algorithm : 유클리드 호제법으로 최대공약수(GCD)를 구해보자 (0) | 2023.02.12 |
|---|---|
| [알고리즘] Floyd-Warshall Algorithm : 플로이드 워셜 알고리즘이란? (2) | 2023.02.04 |
| [알고리즘] Dijkstra Algorithm : 다익스트라(데이크스트라) 알고리즘이란? (0) | 2023.01.25 |
| [알고리즘] BFS (Breadth-First Search) : 너비 우선 탐색 알고리즘이란? (6) | 2023.01.24 |
| [알고리즘] DFS (Depth-First Search) : 깊이 우선 탐색 알고리즘이란? (3) | 2023.01.13 |


