olrlobt
[알고리즘] Dijkstra Algorithm : 다익스트라(데이크스트라) 알고리즘이란? 본문
다익스트라 알고리즘 (Dijkstra Algorithm)
다익스트라 알고리즘 (또는 데이크스트라 알고리즘)은 그래프에서 두 노드 사이의 최단 경로를 찾는 알고리즘이며, BFS와 DP를 사용하여 구현된다.
다익스트라 알고리즘은 일반적으로 두 노드 사이의 가장 짧은 경로를 찾는 문제에 사용되지만, 최단 경로 트리를 만드는 문제에도 많이 사용된다.
BFS와 DP에 대한 이해가 부족하다면, 아래의 포스팅을 통하여 이해를 하면 좋을 것 같다.
BFS :
https://olrlobt.tistory.com/41
[알고리즘] BFS (Breadth-First Search) : 너비 우선 탐색 알고리즘이란?
너비 우선 탐색 BFS(Breadth-First Search) 트리나 그래프를 탐색하는 기법 중 하나로, 시작 노드로부터 자식 노드들을 순서대로 탐색하면서 너비를 우선으로 탐색하는 알고리즘이다. BFS는 완전탐색 알
olrlobt.tistory.com
DP:
https://olrlobt.tistory.com/29
[알고리즘] 동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming)
동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming) DP는 하나의 큰 문제를 작은 문제로 나눈 뒤, 기억하여 푸는 알고리즘 기법이다. DP에서 동적계획법, 동적프로그래밍이라는 단어는, DP 창시
olrlobt.tistory.com
다익스트라 알고리즘 탐색과정
다익스트라 알고리즘의 탐색과정은 크게 인접 행렬 방식과, 우선순위 큐 방식으로 나누어진다.
다음은 다익스트라 알고리즘의 일반적인 탐색과정으로, 정확한 구현은 문제 및 사용된 데이터 구조에 따라 다를 수 있다.
인접 행렬
- 그래프를 나타내기 위해 인접 행렬을 초기화한다.
- 소스 노드의 거리 DP를 0으로 설정하고 다른 모든 노드의 거리 DP를 무한대로 초기화한다.
- 방문을 표시하는 boolean 배열을 만들고 모든 요소를 false로 초기화한다.
- 소스 노드부터 시작하여 모든 노드를 반복한다.
- 현재 노드를 방문한 것으로 표시한다.
- 현재 노드의 각 이웃에 대해:
- 이웃을 방문하지 않은 경우:
- 현재 노드를 통한 이웃까지의 거리가 이웃의 현재 거리보다 작으면 이웃의 거리를 업데이트한다.
- 이웃을 방문하지 않은 경우:
- 모든 노드를 방문할 때까지 4단계를 반복한다.
- 알고리즘이 완료되면 각 노드의 거리는 소스 노드에서 해당 노드까지의 최단 경로 거리를 나타낸다.
우선순위 큐
- 소스 노드의 거리 DP를 0으로 초기화하고 다른 모든 노드의 거리 DP를 무한대로 초기화한다.
- 소스 노드와의 거리를 우선순위로 하는 우선순위 큐를 생성하고 모든 노드를 추가한다.
- 우선순위 큐가 비어 있지 않은 동안:
- 우선순위 큐에서 거리가 가장 짧은 노드를 제거한다.
- 현재 노드의 각 이웃에 대해:
- 현재 노드를 통한 이웃까지의 거리가 이웃의 현재 거리보다 작으면 이웃의 거리를 업데이트한다.
- 새 거리로 이웃을 우선순위 대기열에 추가한다.
- 알고리즘이 완료되면 각 노드의 거리는 소스 노드에서 해당 노드까지의 최단 경로 거리를 나타낸다.
두 방식 중 우선순위 큐 방식이 시간복잡도 방면에서 더욱 효율적이기 때문에, 비교적 많이 사용된다.
다익스트라 알고리즘의 탐색 과정을 애니메이션으로 이해해 보기
간단하게 A - E의 최단거리를 구하는 문제이다.

먼저 시작 노드인 A를 방문처리 해준다.

다음으로 시작 노드 A와 가장 가까이 위치한 C 노드로 이동하고, 방문처리한다.
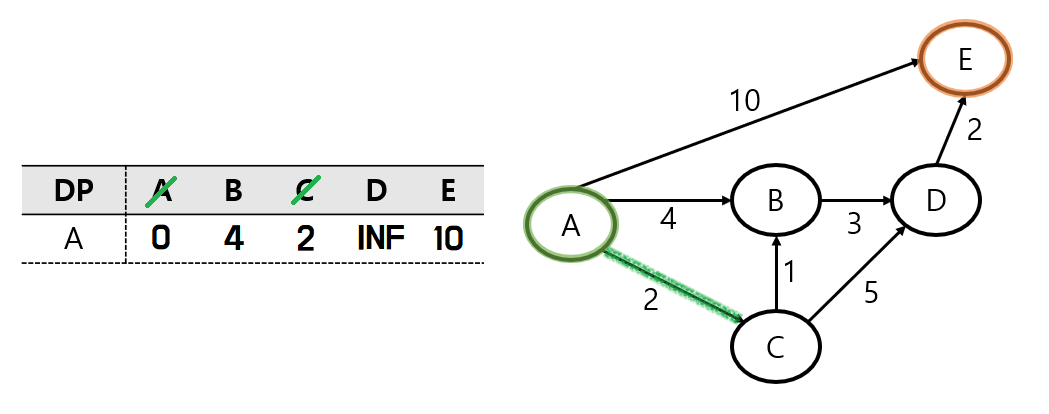
이동한 C 노드에서는 B 노드와 D 노드로 이동을 할 수 있다.
먼저 B노드로 이동을 해보자.
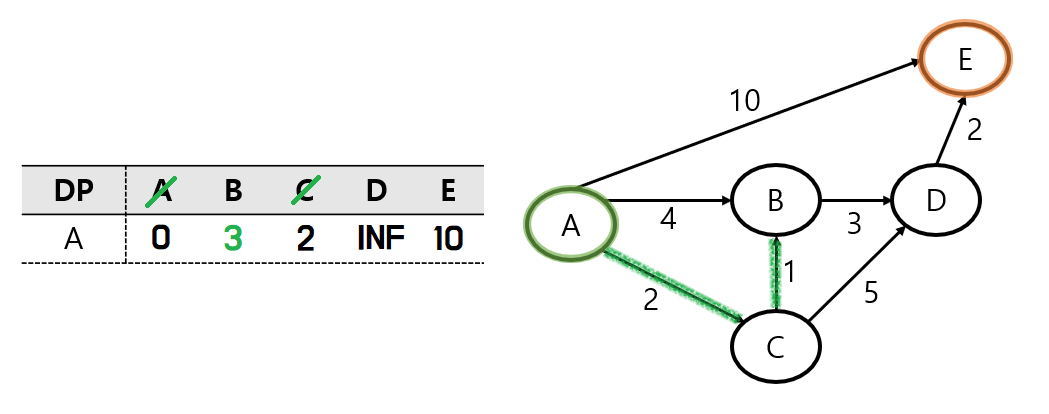
B 노드로 이동을 하게 되면,
DP에 저장된 값인 A - B 경로의 거리 4 보다
위의 그림의 초록색 길인 A - C - B 경로의 거리 3이 더 가까운 거리가 된다.
따라서 DP를 업데이트해 준다.

마찬가지로 C노드에서 D 노드로 가준다.
DP에 저장된 값인 A - D는 직접적으로 이동할 수 없는 값인 INF로 표현이 되어있다. (INF는 엄청 큰 수이다.)
이 값은, A - C - D의 경로를 이동한 7보다 큰 값이므로, DP를 업데이트해 준다.
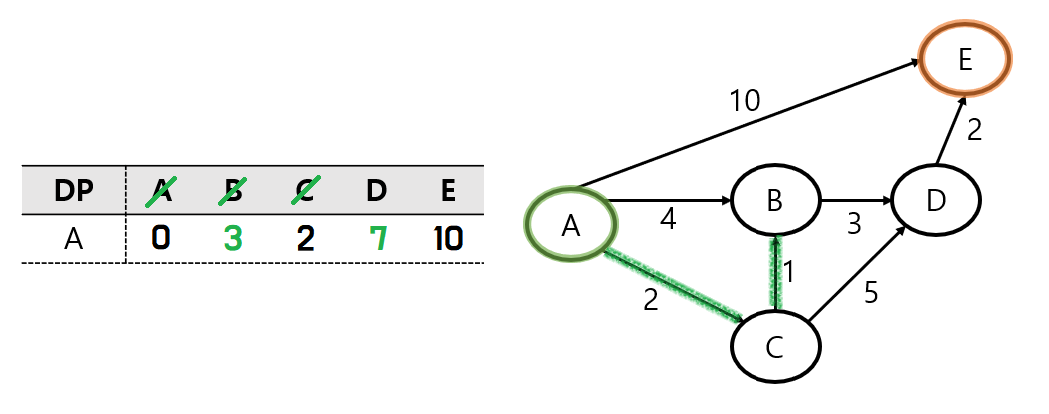
C 노드의 탐색이 끝났으므로, 다음으로 A노드와 가까운 노드인 B 노드를 탐색한다.
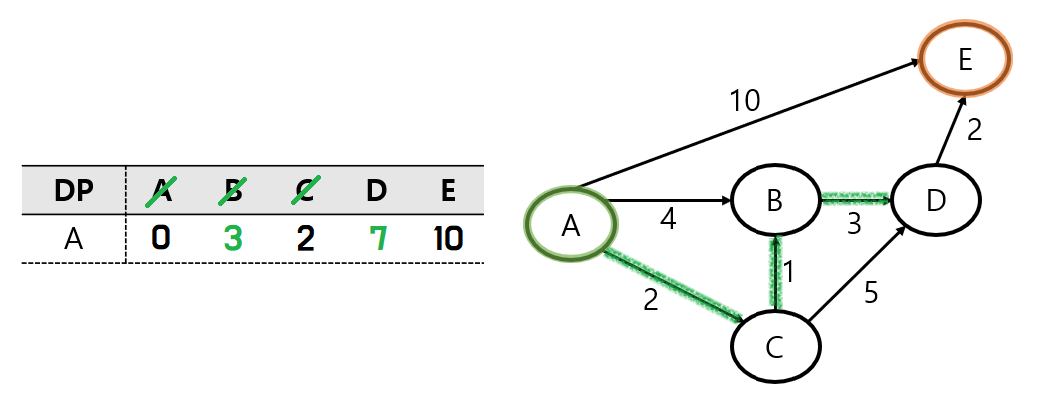
B 노드에서는 D노드로의 경로밖에 없다.
현재 DP에 저장되어 있는 A - D는 이전에 구해놓은 D까지의 최단거리이다.
하지만, B 노드에서 D 노드를 거치는 거리가 6으로 저장된 값보다 작기 때문에 업데이트해 준다.
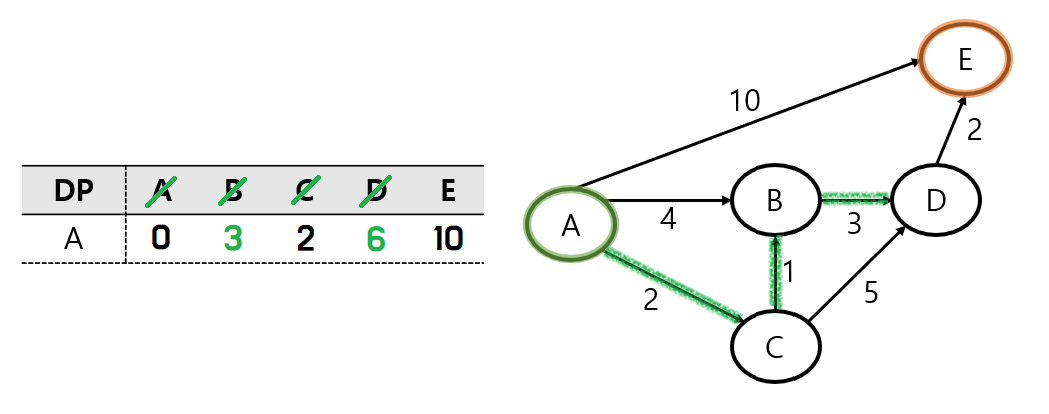
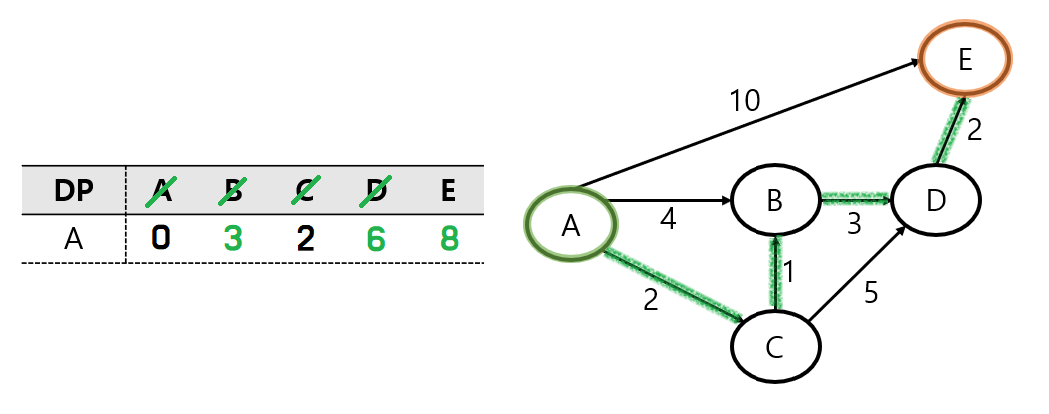
마찬가지로 D 노드를 방문처리하고, 위와 같은 방식으로 처리하면 최종 결과가 나오게 된다.
다익스트라 알고리즘의 장단점
다익스트라의 장점 :
- 인접 행렬 또는 우선순위 대기열을 사용하여 구현할 수 있으므로 가능한 모든 경로를 확인하는 무차별 접근 방식보다 효율적이다.
- 거리뿐만 아니라 경로를 추적하도록 알고리즘을 쉽게 수정할 수 있다.
다익스트라의 단점:
- 음수 가중치 간선을 갖는 그래프에서는 작동하지 않는다.
- 우선순위 대기열을 사용할 때 간선이 많은 큰 그래프의 경우 느려질 수 있다.
- 그래프와 거리를 저장하려면 많은 양의 메모리가 필요하다.
- 동일한 거리에 여러 경로가 있는 경우 최상의 경로를 보장하지 않는다.
- 지형이나 교통 상황과 같은 다른 요소는 고려하지 않는다.
Dijkstra의 알고리즘은 최단 경로 문제를 해결하기 위해 널리 사용되는 알고리즘이지만 모든 상황에서 최선의 선택이 아닐 수 있다.
다익스트라 알고리즘의 구현방법
인접 행렬 방식 구현
public class Dijkstra {
static final int INF = Integer.MAX_VALUE;
static int[][] graph = {{0, 2, 5, INF, INF}, {INF, 0, 1, 4, INF}, {INF, INF, 0, 2, 3}, {INF, INF, INF, 0, 1}, {INF, INF, INF, INF, 0}};
static int[] dist;
static int[] prev;
static boolean[] visited;
public static void dijkstra(int start) {
// Initialize the distance array and the priority queue
dist = new int[graph.length];
Arrays.fill(dist, INF);
dist[start] = 0;
prev = new int[graph.length];
Arrays.fill(prev, -1);
visited = new boolean[graph.length];
for (int i = 0; i < graph.length; i++) {
int u = minDistance();
visited[u] = true;
for (int v = 0; v < graph.length; v++) {
if (!visited[v] && graph[u][v] != 0 && dist[u] != INF && dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
prev[v] = u;
}
}
}
}
public static int minDistance() {
int min = INF, min_index = -1;
for (int v = 0; v < graph.length; v++)
if (!visited[v] && dist[v] <= min) {
min = dist[v];
min_index = v;
}
return min_index;
}
public static void main(String[] args) {
dijkstra(0); //start at node 0
//print the shortest path distance from node 0 to all other nodes
for(int i = 0; i < dist.length; i++) {
System.out.println("Shortest path distance from node 0 to node " + i + " : " + dist[i]);
}
System.out.println("prev[] :" + Arrays.toString(prev));
}
}
우선순위 큐 방식 구현
import java.util.*;
public class Dijkstra {
static final int INF = Integer.MAX_VALUE;
static ArrayList<ArrayList<Pair<Integer, Integer>>> graph = new ArrayList<>();
static int[] dist;
static int[] prev;
static boolean[] visited;
public static void dijkstra(int start) {
// Initialize the distance array and the priority queue
dist = new int[graph.size()];
Arrays.fill(dist, INF);
dist[start] = 0;
PriorityQueue<Pair<Integer, Integer>> pq = new PriorityQueue<>((a, b) -> a.getValue() - b.getValue());
pq.offer(new Pair<>(start, 0));
prev = new int[graph.size()];
Arrays.fill(prev, -1);
visited = new boolean[graph.size()];
while (!pq.isEmpty()) {
Pair<Integer, Integer> p = pq.poll();
int current = p.getKey();
if (visited[current]) {
continue;
}
visited[current] = true;
// Visit the neighbors of the current node
for (Pair<Integer, Integer> neighbor : graph.get(current)) {
int next = neighbor.getKey();
int weight = neighbor.getValue();
if (dist[current] + weight < dist[next]) {
dist[next] = dist[current] + weight;
prev[next] = current;
pq.offer(new Pair<>(next, dist[next]));
}
}
}
}
public static void main(String[] args) {
// Initialize the graph
for (int i = 0; i < 5; i++) {
graph.add(new ArrayList<>());
}
graph.get(0).add(new Pair<>(1, 2));
graph.get(0).add(new Pair<>(2, 5));
graph.get(1).add(new Pair<>(2, 1));
graph.get(1).add(new Pair<>(3, 4));
graph.get(2).add(new Pair<>(3, 2));
graph.get(2).add(new Pair<>(4, 3));
graph.get(3).add(new Pair<>(4, 1));
dijkstra(0); //start at node 0
//print the shortest path distance from node 0 to all other nodes
for(int i = 0; i < dist.length; i++) {
System.out.println("Shortest path distance from node 0 to node " + i + " : " + dist[i]);
}
System.out.println("prev[] :" + Arrays.toString(prev));
}
}
class Pair<K, V> {
private K key;
private V value;
public Pair(K key, V value) {
this.key = key;
this.value = value;
}
public K getKey() {다익스트라 예시 문제
추후에 추가할 예정이다.
'Algorithm > 알고리즘 종류' 카테고리의 다른 글
| [알고리즘] Euclidean Algorithm : 유클리드 호제법으로 최대공약수(GCD)를 구해보자 (0) | 2023.02.12 |
|---|---|
| [알고리즘] Floyd-Warshall Algorithm : 플로이드 워셜 알고리즘이란? (2) | 2023.02.04 |
| [알고리즘] BFS (Breadth-First Search) : 너비 우선 탐색 알고리즘이란? (5) | 2023.01.24 |
| [알고리즘] DFS (Depth-First Search) : 깊이 우선 탐색 알고리즘이란? (2) | 2023.01.13 |
| [알고리즘] 완전탐색 : 브루트포스 알고리즘 Brute Force Algorithm (0) | 2023.01.12 |


