olrlobt
[알고리즘] DFS (Depth-First Search) : 깊이 우선 탐색 알고리즘이란? 본문
깊이 우선 탐색(DFS, Depth-First Search)
트리나 그래프를 탐색하는 기법 중 하나로, 시작 노드에서 자식의 노드들을 순서대로 탐색하면서 깊이를 우선으로 탐색하는 알고리즘이다.
깊이를 우선시하여 모든 경우의 수를 탐색하기 때문에, 완전탐색 알고리즘에 속하기는 하지만,
항상 완전탐색으로 사용되지는 않는다.
DFS는 주로 반복문을 활용하거나, 재귀문을 통하여 구현된다.
DFS의 탐색 과정
DFS의 기본 탐색 과정은 특정 정점에서 시작하여 역추적(backtracking) 하기 전에 각 분기를 따라 가능한 한 멀리 탐색하는 것이다. 탐색하는 과정은 다음과 같다.
- 현재 노드를 방문한 것으로 표시한다.
- 방문한 표시가 되어 있지 않은 각각의 인접한 정점을 탐색한다.
- 더 이상 방문하지 않은 정점이 없으면 이전 정점으로 역추적(backtracking) 한다.
- 모든 정점을 방문할 때까지 프로세스를 반복한다.
DFS의 탐색 방법을 이해하기 위해 아래 애니메이션을 보자.
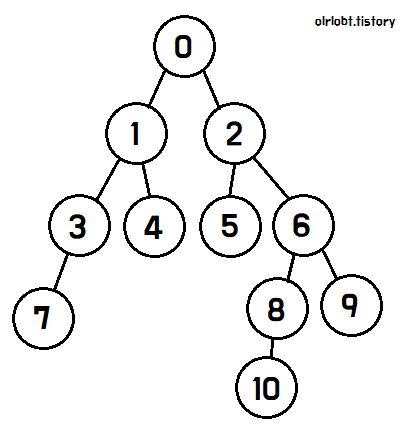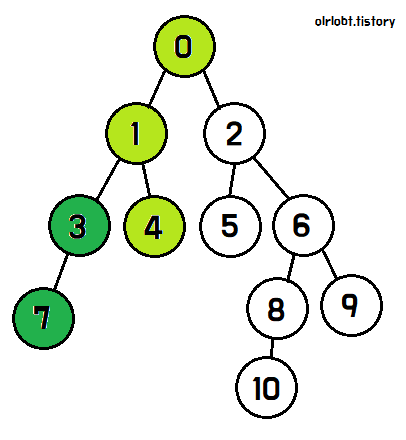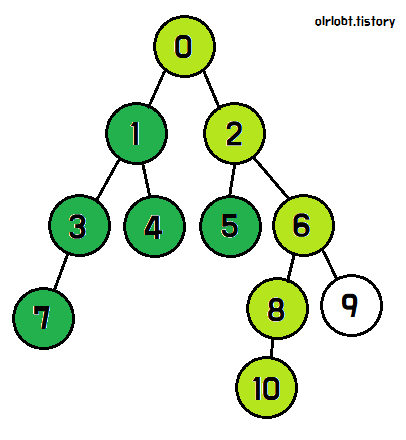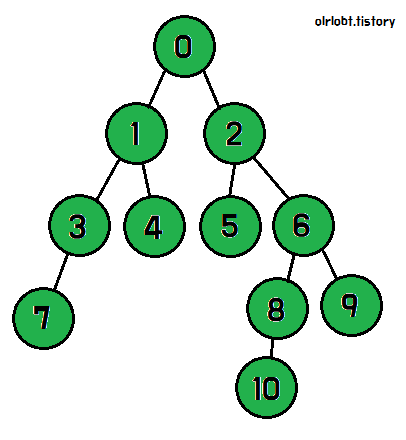
먼저 0번 노드에서 탐색을 시작하면, 자식 노드인 1과 2를 탐색할 수 있다.
1번 노드를 탐색하기로 결정하면, 1번 노드를 완벽히 탐색하기 전까지는 2번 노드를 탐색하지 않는다.
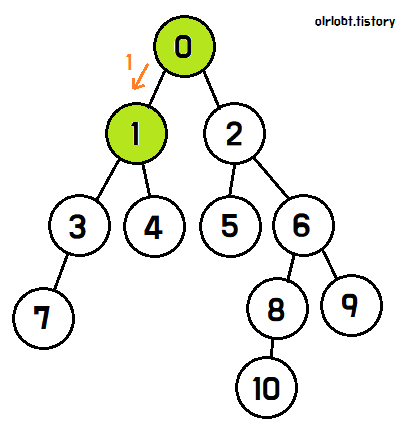
1번 노드에서도, 자식 노드인 3과 4를 탐색할 수 있고,
3번 노드를 완전히 탐색하기 전까지는 4번 노드를 탐색하지 않는다.
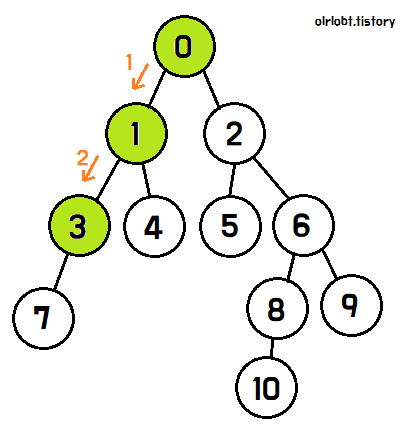
3번 노드는 자식이 7번뿐이므로, 7번을 탐색하고 탐색이 완료되면 탐색완료 표시를 한 뒤, 3번 노드로 돌아간다.
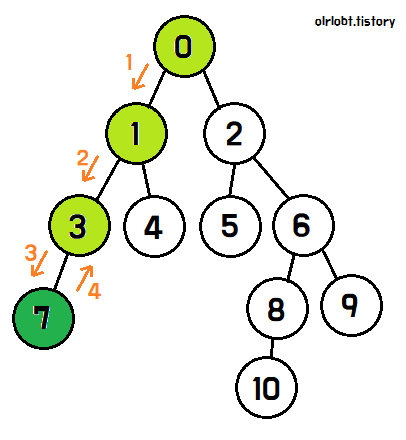
마찬가지로 3번 노드의 탐색이 끝났기 때문에 탐색 완료 표시를 한 뒤, 1번 노드로 돌아간다.
이후, 1번의 남은 자식노드인 4번을 탐색한다.
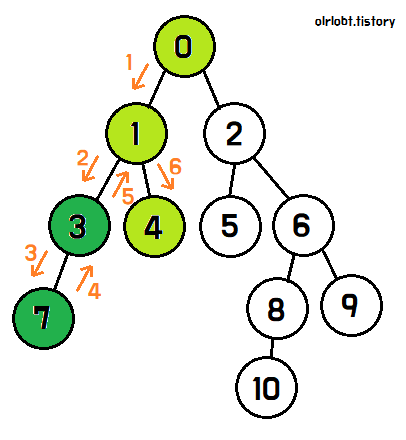
4번의 탐색이 끝나면, 1번의 탐색이 끝났으므로 0번 노드로 돌아간다.
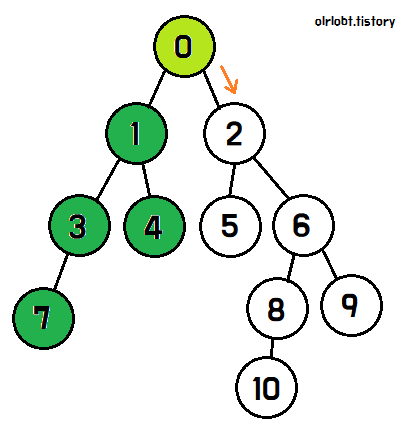
이제 1번 노드의 탐색이 모두 끝난 것이다. 나머지 2번 노드 역시 위와 같은 방식으로 진행하면, 모든 노드를 탐색할 수 있다.
DFS의 장단점
DFS의 장점:
- DFS는 현재 순회 중인 정점만 저장하는 스택 데이터 구조를 사용하기 때문에 BFS에 비해 메모리 공간을 덜 차지한다.
- DFS는 목표가 특정 정점(또는 모든 정점)에 최대한 빨리 도달하는 것일 때 유용하다.
- DFS를 사용하여 그래프에서 순환을 감지할 수 있다.
DFS의 단점:
- 순환 그래프의 경우 DFS가 무한 루프에 빠질 수 있다.
- DFS는 두 정점 사이의 최단 경로를 찾으려는 경우 사용하기에 가장 좋은 알고리즘이 아닐 수 있다.
DFS는 특정 시나리오에서 매우 유용할 수 있지만 항상 최선의 선택은 아니다. 해결하려는 특정 문제에 따라 BFS(Breadth-first Search)와 같은 다른 알고리즘이 더 적합할 수 있다.
DFS 구현 방법
반복 구현 ( Stack 활용) :
반복구현에서는 스택 데이터 구조를 사용하여 방문할 정점을 추적한다.
- 알고리즘은 임의의 정점에서 시작하여 방문한 것으로 표시하고 스택에 푸시한다.
- 스택에서 맨 위 정점을 가져온다.
- 방문하지 않은 모든 인접 정점을 방문하여 방문한 것으로 표시하고 스택으로 푸시한다.
- 스택이 비워질 때까지 프로세스를 반복한다.
import java.util.*;
class DFS {
static ArrayList<Integer>[] adj; // adjacency list representation of the graph
static boolean[] visited; // array to keep track of visited vertices
public static void dfs(int v) {
Stack<Integer> stack = new Stack<>();
stack.push(v);
visited[v] = true;
while (!stack.isEmpty()) {
int vertex = stack.pop();
System.out.print(vertex + " ");
for (int neighbor : adj[vertex]) {
if (!visited[neighbor]) {
stack.push(neighbor);
visited[neighbor] = true;
}
}
}
}
public static void main(String[] args) {
int n = 5; // number of vertices
adj = new ArrayList[n];
visited = new boolean[n];
// initialize adjacency list and visited array
for (int i = 0; i < n; i++) {
adj[i] = new ArrayList<>();
visited[i] = false;
}
// add edges to the graph
adj[0].add(1);
adj[0].add(2);
adj[1].add(2);
adj[2].add(0);
adj[2].add(3);
adj[3].add(3);
for (int i = 0; i < n; i++) {
if (!visited[i]) {
dfs(i);
}
}
}
}
재귀 구현 :
재귀 구현에서는 재귀 함수를 사용하여 그래프의 모든 정점을 방문한다.
이 함수는 현재 정점과 방문한 집합을 입력으로 사용하고 아직 방문하지 않은 모든 인접 정점에 DFS를 적용한다. 재귀는 모든 정점을 방문하는 사례에서 유용하다.
import java.util.*;
class DFS {
static ArrayList<Integer>[] adj; // adjacency list representation of the graph
static boolean[] visited; // array to keep track of visited vertices
public static void dfs(int v) {
visited[v] = true;
System.out.print(v + " ");
for (int neighbor : adj[v]) {
if (!visited[neighbor]) {
dfs(neighbor);
}
}
}
public static void main(String[] args) {
int n = 5; // number of vertices
adj = new ArrayList[n];
visited = new boolean[n];
// initialize adjacency list and visited array
for (int i = 0; i < n; i++) {
adj[i] = new ArrayList<>();
visited[i] = false;
}
// add edges to the graph
adj[0].add(1);
adj[0].add(2);
adj[1].add(2);
adj[2].add(0);
adj[2].add(3);
adj[3].add(3);
for (int i = 0; i < n; i++) {
if (!visited[i]) {
dfs(i);
}
}
}
}
두 방법 모두 시간 및 공간 복잡도는 동일하지만 반복 구현은 일반적으로 호출 스택을 사용하지 않기 때문에 공간 측면에서 더 효율적이라고 간주된다.
보다시피 재귀 구현은 반복 구현보다 더 간단하고 간결하며 읽기 쉽다. 하지만, 그래프가 커지거나 순환이 있는 경우 재귀를 사용하면 스택 오버플로가 발생할 수 있다. 이런 경우에는 반복 구현이 더 적합하다.
DFS 예시 문제
https://www.acmicpc.net/problem/1240
1240번: 노드사이의 거리
N(2≤N≤1,000)개의 노드로 이루어진 트리가 주어지고 M(M≤1,000)개의 두 노드 쌍을 입력받을 때 두 노드 사이의 거리를 출력하라.
www.acmicpc.net
https://www.acmicpc.net/problem/2251
2251번: 물통
각각 부피가 A, B, C(1≤A, B, C≤200) 리터인 세 개의 물통이 있다. 처음에는 앞의 두 물통은 비어 있고, 세 번째 물통은 가득(C 리터) 차 있다. 이제 어떤 물통에 들어있는 물을 다른 물통으로 쏟아 부
www.acmicpc.net
https://www.acmicpc.net/problem/2668
2668번: 숫자고르기
세로 두 줄, 가로로 N개의 칸으로 이루어진 표가 있다. 첫째 줄의 각 칸에는 정수 1, 2, …, N이 차례대로 들어 있고 둘째 줄의 각 칸에는 1이상 N이하인 정수가 들어 있다. 첫째 줄에서 숫자를 적절
www.acmicpc.net
'Algorithm > 알고리즘 종류' 카테고리의 다른 글
| [알고리즘] Dijkstra Algorithm : 다익스트라(데이크스트라) 알고리즘이란? (0) | 2023.01.25 |
|---|---|
| [알고리즘] BFS (Breadth-First Search) : 너비 우선 탐색 알고리즘이란? (5) | 2023.01.24 |
| [알고리즘] 완전탐색 : 브루트포스 알고리즘 Brute Force Algorithm (0) | 2023.01.12 |
| [알고리즘] 동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming) (0) | 2023.01.05 |
| [알고리즘] 탐욕법 : 그리디 알고리즘 Greedy Algorithm (0) | 2023.01.03 |



