olrlobt
[알고리즘] Floyd-Warshall Algorithm : 플로이드 워셜 알고리즘이란? 본문
플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)
Floyd-Warshall 알고리즘은 음수 순환 사이클이 없는 그래프에서, 모든 점에서 모든 점까지의 최단거리를 구하는 알고리즘이다.
한 점에서 이웃 노드를 탐색하며 최단 거리를 구하는 다익스트라 알고리즘과는 다르게,
거쳐가는 중간 노드를 기준으로 최단 거리를 구한다.
또한, 다익스트라 알고리즘과 다르게, 음의 가중치를 갖는 간선이 있어도 된다.
하지만, 합이 음수 가중치를 갖는 사이클이 있어서는 안 된다.

위 그림은 1에서 4로 가는 최단 경로를 구하려 한다.
양쪽 그림 모두 2 > 3 > 2로 가는 사이클이 존재하지만, 좌측은 합이 +1, 우측은 합이 -1이다.
위 문제를 해결하기 위해서 좌측 그림은 1 > 2 > 4의 경로로 해결하면 되지만,
우측 그림의 경우에는 2 > 3 > 2 한 번의 사이클을 돌 때마다, 최단경로가 1씩 단축이 되어버린다.
따라서, 합이 음의 가중치인 사이클을 갖는 그래프에서는 최단 경로를 구할 수 없다.
플로이드 워셜은 DP 동적계획법 기술에 의거하기에, DP의 이해가 부족하다면 아래의 포스팅을 참조하고 오자.
DP:
https://olrlobt.tistory.com/29
[알고리즘] 동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming)
동적계획법 : 다이나믹 프로그래밍 DP (Dynamic programming) DP는 하나의 큰 문제를 작은 문제로 나눈 뒤, 기억하여 푸는 알고리즘 기법이다. DP에서 동적계획법, 동적프로그래밍이라는 단어는, DP 창시
olrlobt.tistory.com
참고로,
플로이드-워셜 알고리즘의 이름은 플로이드와 워셜이 만든 알고리즘이기 때문이라고 한다.
플로이드 워셜 탐색과정
- DP 2차원 배열을 각 정점 사이의 가중치로 초기화한다. 가중치가 없는 경우 INF (Integer.MAX_VALUE)로 설정한다.
- 각 중간 정점 k에 대하여 시작 정점 i와 끝 정점 j의 가능한 모든 조합을 반복문으로 탐색한다.
- (현재 거리 > 중간 정점 k를 거친 거리 ) 이면 DP를 업데이트한다.
- 그래프의 모든 정점에 대해 2- 3단계를 반복한다.
플로이드 워셜 탐색과정을 애니메이션으로 이해해 보기
이 전 게시글인 다익스트라 알고리즘에서와 같은 예시이다.
풀어지는 과정을 비교해 보면 좋을 것 같다.

플로이드 워셜은, 앞서 말했듯이 중간 노드(거쳐가는 노드)를 기준으로 탐색하는 방법이다.
맨 첫 거쳐가는 노드인 A는 A로 도착하는 화살표가 없어, 거쳐가는 노드가 될 수 없으므로 넘어간다.

두 번째로, B 노드를 거쳐가는 노드로 본다면, A - B와 B - D를 확인할 수 있고, 이는 기존 A - D 보다 작은 값이므로 DP를 업데이트한다.
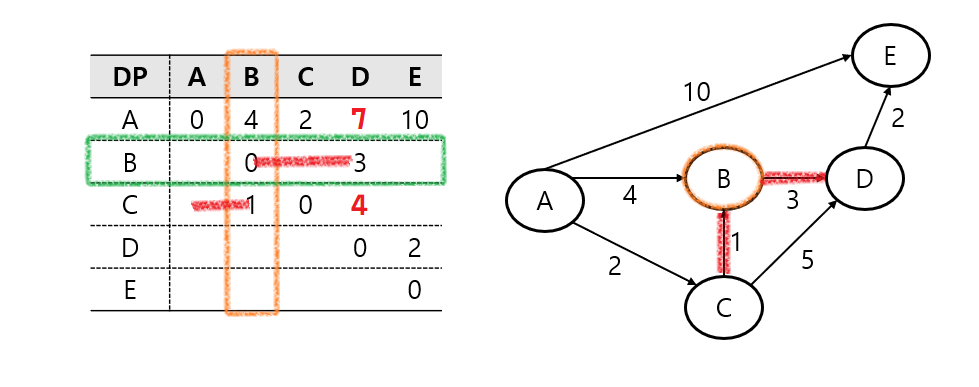
다음으로 C - B와 B - D를 확인할 수 있고, 이는 기존 C - D 보다 작은 값이기 때문에 DP를 업데이트한다.
B노드로 도착하는 노드가 없으므로, B 노드의 탐색을 마쳤다.
다음 거쳐가는 노드는 C 노드이다.
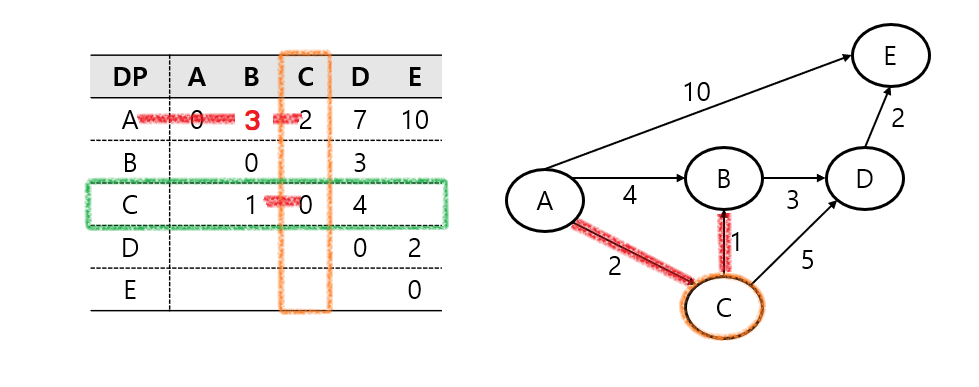
A - C와 C - B의 합은 A - B 보다 작다. DP를 업데이트한다.
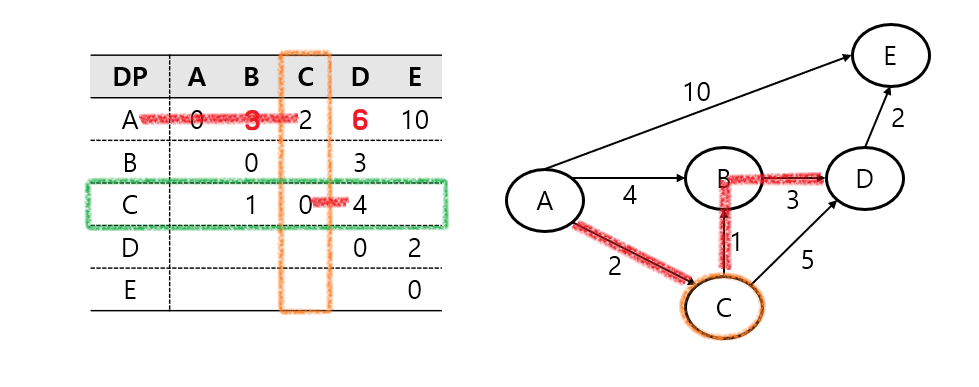
마찬가지로 A - C와 C - D를 합할 차례이다.
여기서, C - D는 앞의 과정에서 이미 최단 거리를 계산했기 때문에, 오른쪽과 같은 그림과 같이 나타낼 수 있고,
DP에는 이미 최단거리가 저장되어 있기 때문에, DP 값 계산만 해 주면 된다.
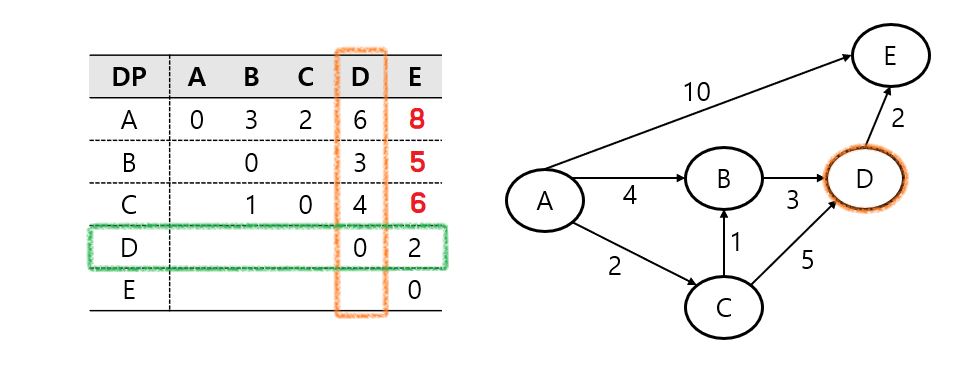
남은 D와 E도 똑같은 과정을 반복하면, 위와 같은 결과가 도출된다.
플로이드 워셜 시간복잡도와 공간복잡도
플로이드 워셜은 3중 반복문을 사용한다.
시간복잡도 : O(n^3)
DP를 사용할 때, N x N 크기의 2차원 배열을 사용한다.
공간복잡도 : O(n^2)
이때, n = 그래프 정점의 수이다.
플로이드 워셜 장단점
플로이드 워셜 장점:
- Dijkstra의 알고리즘과 달리 가중치가 음수여도 처리할 수 있다.
- 방향 그래프와 무방향 그래프 모두에서 작동한다.
- 구현하고 이해하는 것이 매우 간단하다.
플로이드 워셜 단점:
- 시간 복잡도는 O(n^3)이므로 큰 그래프의 경우 속도가 느려진다.
- 중간 결과를 저장하려면 많은 양의 메모리를 필요로 한다.
- 가중치의 합이 음수인 사이클을 갖는 그래프에서는 작동하지 않는다.
플로이드 워셜 알고리즘 자바 구현
플로이드 워셜 알고리즘은 3중 반복문으로 구현이 되고,
이 3중 반복문은 각각 다음을 나타낸다.
k = 중간 거점
i = 시작 노드
j = 도착 노드
import java.util.Scanner;
public class FloydWarshall {
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(); // number of vertices
int m = scanner.nextInt(); // number of edges
int[][] dist = new int[n][n];
// initialize distance matrix
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
dist[i][j] = 0;
} else {
dist[i][j] = INF;
}
}
}
// read edges and update distance matrix
for (int i = 0; i < m; i++) {
int from = scanner.nextInt();
int to = scanner.nextInt();
int weight = scanner.nextInt();
dist[from][to] = weight;
}
// floyd-warshall algorithm
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] != INF && dist[k][j] != INF) {
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
// print the shortest distances
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(dist[i][j] + " ");
}
System.out.println();
}
}
}
플로이드 워셜 예제 문제
추후에 추가 예정이다.
참고 사이트
'Algorithm > 알고리즘 종류' 카테고리의 다른 글
| [알고리즘] Divide and Conquer Algorithm : 분할정복 알고리즘을 알아보자 (0) | 2023.02.19 |
|---|---|
| [알고리즘] Euclidean Algorithm : 유클리드 호제법으로 최대공약수(GCD)를 구해보자 (0) | 2023.02.12 |
| [알고리즘] Dijkstra Algorithm : 다익스트라(데이크스트라) 알고리즘이란? (0) | 2023.01.25 |
| [알고리즘] BFS (Breadth-First Search) : 너비 우선 탐색 알고리즘이란? (5) | 2023.01.24 |
| [알고리즘] DFS (Depth-First Search) : 깊이 우선 탐색 알고리즘이란? (2) | 2023.01.13 |


