olrlobt
[프로그래머스 2단계] 예상 대진표 본문
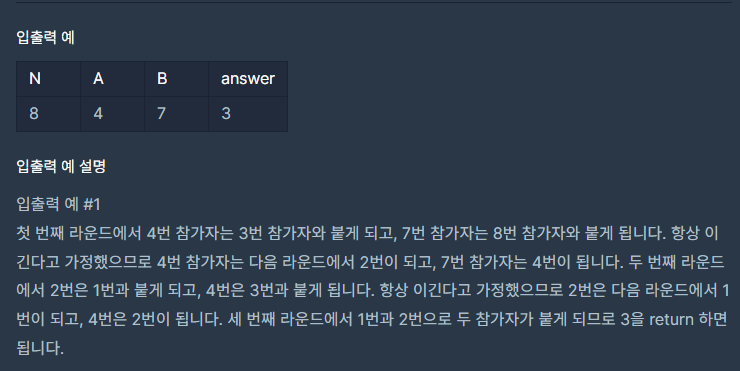
🔒 2단계 - 예상 대진표

📌 테스트케이스 추가 힌트
이번 문제는 일반적인 테스트 케이스만 추가하면 된다.
✍️ 풀이법
먼저 해당 문제를 쉽게 와닿게 하고, 푸는 방법을 머릿속에 그리기 위해
해당 문제의 예시들 중 간단히 그릴수 있는 예시 몇가지를 그려보았다.
a=4 b=7 result=3
ex)
?
4 7
1 4 5 7
1 2 3 4 5 6 7 8
a=5 b=7 result=2
ex)
4 ?
1 4 5 7
1 2 3 4 5 6 7 8
여기서 떠올린 점은
주어지는 N을 반으로 선을 그어 나누면, 또 다른 토너먼트 그룹 2가지로 나누어지게 되고,
다른 그룹에 있다면 무조건 맨 위에서 만난다는 점이었다.
예를들어 아래의 그림에서, a가 line(2/n) 을 기준으로 좌측에 있따면, 우측의 5,6,7,8 을
만나기 위해서는 꼭대기까지 가야한다.
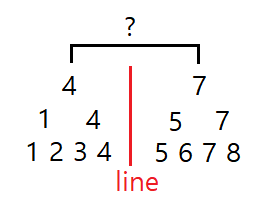
이 방법과 주어진 n이 2의 지수승으로 최대값을 알려주고 있으니,
a와 b의 위치를 line 으로 식별해서 반복해 나가면 된다.
여기서 생각해야 할 점은 line의 오른쪽 그룹을 가져가게 될 경우,
5,6,7,8 이라는 숫자를 어떻게 가져갈 것인가. 이었는데
이는 간단히 오른쪽 그룹을 왼쪽 그룹으로 만드는 것으로 해결했다.( 5,6,7,8 에서 line 인 4 를 빼주는 방법)
🗝️ 풀이
class Solution
{
public int solution(int n, int a, int b)
{
int answer = 1;
int line = 0;
int count =0;
int m = n;
for(int j = 0; m!=1; j ++){ //n의 지수승 count를 구한다.
m=m/2;
count = j;
}
for(int i=0; n!=1;i++){
line = n/2;
if((a<=line&& b>line) || (b<=line&& a>line)){ //a와 b의 위치가 다르다면
// System.out.println("line" + line);
answer = count-i+1;
break;
}else{ // a와 b의 위치가 같은쪽에 있다면,
if(a>line){ // a가 line 오른쪽에 있다면
a -= line; // 새로운 line 설정을 위해 line만큼 빼주어
b -= line; // 값을 재 설정한다.
}
}
n= line;
}
return answer;
}
}
해당방법으로 문제를 풀고, 다른사람들이 푼 방법을 보았을때,
a,b의 위치에서 시작하는 분들이 많다는 것을 알게 되었다.
내 방법도 나쁘지는 않았다고 생각하지만,
단순히 a와 b가 경쟁구도인것을 계속 검사하면서 올라가면 되는 좋은 방법도 있다는 것을 알게 되었다.
또한, 지수승을 구하기 위한 Math 함수가 있을 것 같은데, 해당 함수를 사용하지 못하여 아쉬움이 남는 문제였다.
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스 2단계] 올바른 괄호 (0) | 2022.12.30 |
|---|---|
| [프로그래머스 2단계] 점프와 순간 이동 (0) | 2022.12.30 |
| [프로그래머스 2단계] 영어 끝말잇기 (0) | 2022.12.30 |
| [프로그래머스 2단계] JadenCase 문자열 만들기 (0) | 2022.12.30 |
| [프로그래머스 0단계] 몫 구하기 (0) | 2022.12.30 |
Comments