olrlobt
[자바/백준 골드5] #2293 동전 1 본문
https://www.acmicpc.net/problem/2293
🔒 골드5 - #2293 동전 1


📌 테스트케이스 추가 힌트
4 10
1
2
5
3
= 20✍️ 풀이법
대표적인 DP 문제이다.
DP 문제를 풀 때, 가장 먼저 고려해야 할 것은
캐싱을 통한 점화식 도출이다.
캐싱을 위해 DP 테이블을 그려보면,
가로축에 K원이 되기 위한 가치를 나열할 수 있다.
그리고 세로축에 동전을 하나씩 추가하며 문제를 해결해 보자.

먼저 1원짜리 동전을 추가한다.
1원짜리 동전으로 1원을 만들던, 2원을 만들던, 3원을 만들던... 값은 모두 1이 되므로 1로 채워지게 된다.
또한, 0원을 만드는 경우도 { x } 동전을 선택하지 않는 경우 1가지로 생각할 수 있다.

다음으로 2원짜리 동전을 추가한다.
2원짜리 동전까지는 쉽게 직접 세어볼 수 있으므로, 채워 놓고 생각해 보면,
2원을 만들기 위해서는 (2) / (1+1) 두 가지 경우가 존재한다.
3원을 만들기 위해서는 (2+1) / (1+1+1) 두 가지 경우가 존재한다
4원을 만들기 위해서는 (2+2) / (2+1+1) / (1+1+1+1) 세 가지 경우가 존재하고,
5원을 만들기 위해서는 (2+2+1) / (2+1+1+1) / (1+1+1+1+1) 세 가지 경우가 존재한다.
1원과 2원 동전만으로는 점화식을 세우기 쉽지 않으므로 다음 경우를 본다.
다음 5원짜리 동전을 추가해 보자.
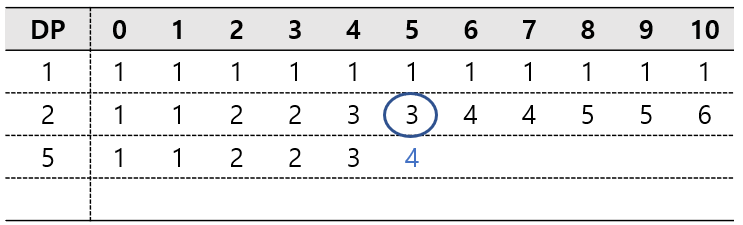
5원짜리 동전이 개입되는 건, 5원을 만들 때부터 이다.
따라서 1~4원을 만드는 가짓수는 이 전의 값을 그대로 가져와서 채워 준다.
5원을 만드는 경우의 수는
5원짜리 동전만으로 만드는 경우 (5) 한 가지와
이 전까지의 동전(1원과 2원) 만으로 만드는 경우 (2+2+1) / (2+1+1+1) / (1+1+1+1+1) 세 가지를 더한
4가지이다.
이 것은,
5원을 포함하지 않는 경우 + 5원을 하나 이상 포함하는 경우로 나눌 수 있는데,
5원을 포함하지 않는 경우는
이 전까지의 동전(1원과 2원) 만으로 만드는 경우로 3가지이고,
5원을 하나 이상 포함하는 경우는
하나 이상 포함되어 있기 때문에 만들고자 하는 돈에서 5원을 빼 준 경우의 수
즉, 만들고자 하는 돈( 5 )에서 현재 동전의 단위 ( 5원 )를 뺀 ( 0)을 만드는 경우이며,
아래 그림처럼 나타낼 수 있다.
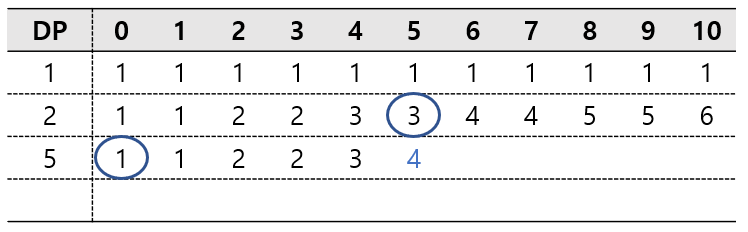
5원이 중복돼서 사용되기 때문에, 5를 뺀 값을 이 전 캐시가 아닌 현재 캐시에서 찾아야 한다.
따라서 3+1=4의 값이 나온다.

마찬가지로, 6원을 만드는 경우의 수는
이 전까지의 동전 (1원과 2원) 4가지와
5원짜리 동전을 사용해 만드는 경우 (5+1) 한 가지.
즉, 5원이 포함 안 된 경우 4가지와
5원으로 1원을 만드는 경우 1가지를 더하면 된다.

마찬가지로,
7원 = 4 + 2 = 6
8원 = 5 + 2 = 7
9원 = 5 + 3 = 8
마지막 10원의 경우,
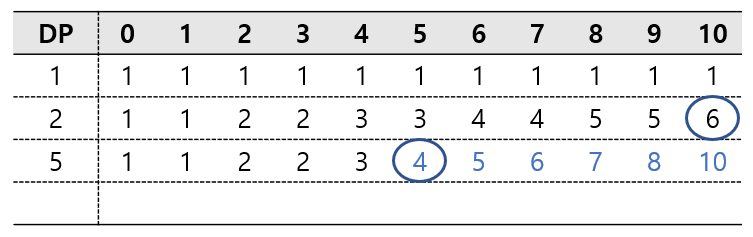
5원을 사용하지 않는 6가지 경우의 수와
5원을 한 번 이상 사용하는 경우.
즉, 10 - 5 = 5 ( 한번 사용했기 때문에 5를 빼준다)
5를 만드는 경우의 수 (이 경우에도 5가 포함될 수 있다. 따라서) 4가지
6+4=10 이 된다.
이해가 가지 않는다면, 테스트케이스 추가 힌트를 보며 위 과정을 한 번 더 수행하길 권장한다.

따라서 점화식은
이차원 배열로는 다음과 같이 나타낼 수 있고,
dp [ i ][ j ] = dp [ i-1 ][ j ] dp [ i ][ j - coin [ i ] ]
일차원 배열로는 다음과 같이 나타낼 수 있다.
dp [ i ] += dp [ i - coin [ j ] ]
🗝️ JAVA 풀이
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class baekjoon2293 {
static int K;
static int N;
static List<Integer> dp = new ArrayList<>();
static int[] P;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
P = new int[N];
for (int testCase = 0; testCase < N; testCase++) {
P[testCase] = sc.nextInt();
}
solve();
}
public static void solve() {
dp.add(0);
for (int i = 0; i < K; i++) {
dp.add(0);
}
dp.set(0,1);
for (int index = 0; index < N; index++) {
for (int j = P[index]; j <= K; j++) {
dp.set(j, dp.get(j) + dp.get(j - P[index]));
}
}
System.out.println(dp.get(K));
}
}
'Algorithm > 백준' 카테고리의 다른 글
| [JAVA/백준 골드5] #2294 동전 2 (2) | 2023.01.11 |
|---|---|
| [자바/백준 골드5] #12865 평범한 배낭 (1) | 2023.01.09 |
| [자바/백준 골드5] #1461 도서관 (1) | 2023.01.02 |
| [자바/백준 골드5] #13164 행복 유치원 (2) | 2023.01.01 |
| [자바/백준 골드3] #13904 과제 (2) | 2022.12.31 |



